Лекция №8 часть 3

Пересечение линии с поверхностью. Взаимное пересечение поверхностей.
Метод вспомогательных секущих плоскостей. Метод вспомогательных секущих сфер.
Частные случаи пересечения поверхностей второго порядка.

Пересечение линии с поверхностью

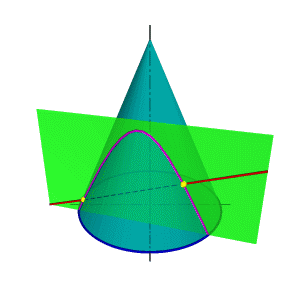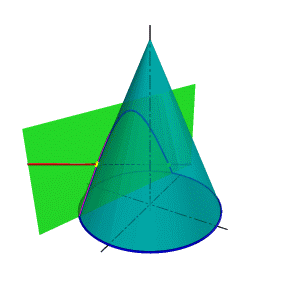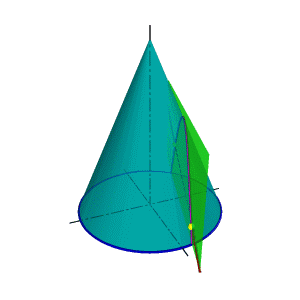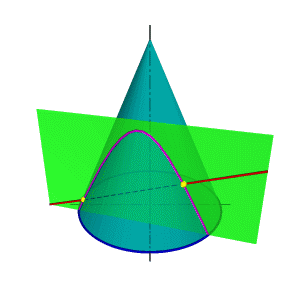
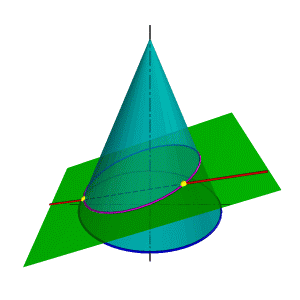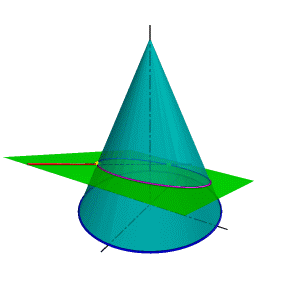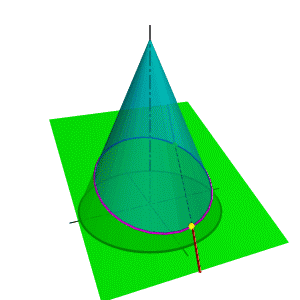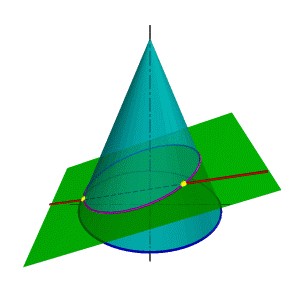
В общем случае для графического определения точек пересечения линии с поверхностью (рис.8.28) необходимо выполнить ряд геометрических построений, описываемых следующим алгоритмом:

1. Заключаем линию l в некоторую вспомогательную поверхность Δ;

1. Строим линию m пересечения данной поверхности Ф и вспомогательной поверхности Δ;

2. Определяем искомую точку К пересечения линии l и m (точка может быть не единственная).

В качестве вспомогательной поверхности целесообразно использовать проецирующую цилиндрическую поверхность, направляющей которой должна служить заданная линия, а –прямолинейными образующими – проецирующие прямые.

Пример: Определить точки пересечения прямой линии с поверхностью конуса вращения и определить видимость прямой по отношению к конусу.

Если в качестве вспомогательной секущей плоскости можно выбрать горизонтально проецирующую или фронтально проецирующую плоскости, то в сечении получатся соответственно гипербола (рис.8.29а) или эллипс (рис.8.29б). Построение кривых линий значительно усложняет задачу.

Рисунок 8.28. Пересечение линии с поверхностью


	а) горизонтально проецирующая плоскость	б) фронтально проецирующая плоскость
Рисунок 8.29 Пересечение прямой линии с конусом (вспомогательная секущая плоскость- проецирующая плоскость )

а) модель

б) эпюр

Рисунок 8.30. Пересечение прямой линии с конусом

(вспомогательная секущая плоскость-плоскость общего положения)

Поэтому в качестве вспомогательной секущей плоскости целесообразно выбрать такую плоскость, которая бы включала прямую l и пересекала конус по образующим (рис.8.30). Очевидно, что такая плоскость определяется прямой l и точкой S- вершиной конуса. Пусть основание конуса лежит в горизонтальной плоскости проекций, тогда линия пересечения вспомогательной секущей плоскости и горизонтальной плоскости проекций ВС пересекает основание конуса в точках D и F. Таким образом в сечении конуса вспомогательной секущей плоскостью получится треугольник DFS. Так как полученный треугольник и прямая l лежат в одной плоскости, точки их пересечения К и М и есть точки пересечения прямой с конусом.

Взаимное пересечение поверхностей

Линией пересечения двух поверхностей является множество точек, общих для данных поверхностей. Из этого множества выделяют характерные (опорные, или главные) точки, с которых следует начинать построение этой линии. Они позволяют увидеть, в каких границах можно изменять положение вспомогательных секущих поверхностей для определения остальных точек.

К таким точкам относятся: экстремальные точки- верхняя и нижняя точки относительно той или иной плоскости проекций; точки, расположенные на очерковых образующих некоторых поверхностей точки границы зоны видимости и т.д.

Следует имеет в виду, что линия пересечения двух поверхностей в проекциях всегда располагается в пределах контура наложения проекций двух пересекающихся поверхностей.

Иногда целесообразно воспользоваться преобразованием чертежа, чтобы представить пересекающиеся поверхности (или одну из них) в частном положении.

Для определения этих точек часто пользуются вспомогательными секущими поверхностями. Поверхности-посредники пересекают данные поверхности по линиям, которые, в свою очередь, пересекаются в точках линии пересечения данных поверхностей.

Секущие поверхности-посредники выбираются так, чтобы они, пересекаясь с данными поверхностями, давали простые для построения линии, например прямые и окружности.

Из общей схемы построения линии пересечения поверхностей выделяют два основных метода - метод секущих плоскостей и метод секущих сфер.

В общем случае решение задачи по построении линии пересечения двух поверхностей может быть сведено к рассмотренным ранее задачам по определению:

1. Точек пересечения линии с поверхностью;

2. Линии пересечения плоскости и поверхности;

3. Комбинации первой и второй задачи.

Метод вспомогательных секущих плоскостей.

Вспомогательные секущие плоскости чаще всего выбирают проецирующими и параллельными одной из плоскостей проекций - плоскостями уровня.

Этот способ рекомендуется применять, если сечения заданных поверхностей одной и той же плоскостью являются прямыми линиями или окружностями. Такая возможность существует в трех случаях:

1. Если образующие (окружности) расположены в общих плоскостях уровня;

2. Если в общих плоскостях уровня оказываются прямолинейные образующие линейчатой поверхности и окружности циклической;

3. Линейчатые каркасы заданных поверхностей принадлежат общим плоскостям уровня или пучкам плоскостей общего положения.

Пример 1: Рассмотрим построение линии пересечения треугольной призмы с конусом (рис.8.31) . Пусть ось вращения конуса перпендикулярна плоскости П₁, а грани призмы перпендикулярны плоскости П₂. В этом случае призму можно рассматривать, как три плоскости *α, β, γ,* проходящие через ее грани, а задача сводится к нахождению линий пересечения этих плоскостей с конусом. При этом в соответствии с характерными сечениями конуса известно, что плоскость α пересекает конус по окружности параллельной П₁, β- по гиперболе параллельной П₃, а γ- по эллипсу. На плоскость П₂ линии пересечения от всех плоскостей проецируются в прямые, совпадающие со следами плоскостей *α, β,* и γ. Для построения проекций этих линий на плоскости П₁ и П₃ отметим характерные точки на уже имеющейся фронтальной проекции линий пересечения:
		а) модель

	б) эпюр
Рисунок 8.31. Пересечение конуса и призмы

Точки 1₂ и 6₂ – пересечения плоскости γ с очерком проекции конуса на плоскость П₂ (главным меридианом), эти точки определяют положение большой оси эллипса, кроме того точка 1₂ –проекция точки вершины гиперболы и одновременно принадлежит конусу (лежит на очерке фронтальной проекции конуса) и ребру призмы (линии пересечения плоскостей α и β), а точка 6₂- проекция точки, одновременно принадлежащей конусу и ребру призмы (линии пересечения плоскостей α и γ); точки 2, 3, 7 и 8 – характерны тем, что их профильные проекции лежат на очерке проекции конуса; 4₂, 5₂- точки, лежащие на середине отрезка 1₂6₂ (большой оси эллипса) и определяют положение малой оси эллипса; 9,10 – точки одновременно принадлежащие конусу и ребру призмы (образованному пересечением плоскостей α и β).

Рассмотрим последовательность нахождения проекций точек 4 и 5. Через фронтальные проекции этих точек проведем вспомогательную секущую плоскость φ. Эта плоскость пересекает конус по параллели p, а грань призмы по прямой линии m, параллельной ребру. На горизонтальной плоскости проекций пересечение p₁ и m₁ определяют положение точек 4₁ и 5₁. Для точного построения кривых линий пересечения поверхностей обозначенных точек не достаточно. После нахождения проекций всех точек их необходимо соединить с учетом видимости.

Пример 2: Пересечение сферы и цилиндра (рис.8.32).В данном примере вспомогательные плоскости уровня могут быть параллельными плоскостям П₂ и П₁. В первом случае фронтальные плоскости пересекают сферу по окружности, а цилиндр по прямолинейным образующим. Одна из таких плоскостей α пересекается с поверхностями по дуге окружности a и прямой линии b. Точка 1 пересечения дуги окружности а и прямой b принадлежат искомой кривой.

	а) модель	б) эпюр
Рисунок 8.32. Пересечение полусферы и эллиптического цилиндра

С помощью вспомогательной секущей плоскости b (плоскости главного фронтального меридиана полусферы) найдены точки 2 и 3, как точки пересечения главного фронтального меридиана полусферы - дуги окружности с с линиями d и g. Плоскость g - плоскость главного фронтального меридиана цилиндра, пересекает полусферу по дуге окружности - k которая в свою очередь пересекаясь с фронтальным меридианом цилиндра l и m определяет положение точек 4 и 5. Аналогично, с помощью плоскости j найдены точки 6 и 7.

Точка 8 найдена с помощью фронтально проецирующей плоскости w, параллельной горизонтальной плоскости проекций, которая пересекает полусферу по окружности - экватору h, а цилиндр по окружности основания s.

Характерными точками, в данном случае, являются точки 1- 5 и 8, лежащие на очерках проекций поверхностей. Кроме того, точки 1 и 8 определяют границу зоны видимости кривой на плоскость П₁, а точки 4 и 5 – границу зоны видимости на плоскость П₂.

Метод вспомогательных секущих сфер.

При определении линии пересечения двух поверхностей вращения, при их особом взаимном расположении, не всегда рационально применять вспомогательные секущие плоскости. В некоторых случаях применяют метод вспомогательных секущих сфер – концентрических или эксцентрических.

Концентрические сферические посредники применяются при определении линии пересечения двух поверхностей вращения с пересекающимися осями. Каждая из этих поверхностей имеет семейство окружностей, являющихся линиями сечения их концентрическими сферами. Применению метода концентрических сфер должно предшествовать такое преобразование чертежа в результате которого оси обеих поверхностей должны быть расположены параллельно одной и той же плоскости проекций (рис.8.33) или одна из осей становиться проецирующей прямой, а вторая - линией уровня (рис.34).

	а) модель	б) эпюр
Рисунок 8.33. Пересечение поверхностей вращения, оси которых параллельны фронтальной плоскости проекций.

Оси поверхностей G и Q параллельны фронтальной плоскости проекций и пересекаются в точки А (рис.8.33). Эта точка принимается за центр всех вспомогательных концентрических сфер. Каждая из концентрических сфер пересекает поверхности по окружностям - параллелям (а, b, c, d, n), фронтальные проекции которых являются прямыми линиями (а₂, b₂, c₂, d₂, n₂). Проекции точек 1₂, 2₂, 3₂, 4₂, 5₂ и 6₂пересечения проекций параллелей принадлежат проекции искомой линии пересечения поверхностей. Пересечение главных меридианов определяет крайние точки 7 и 8.

Для точного построения линии пересечения поверхностей необходимо найти точки 9 и 10, которые определяют границу зоны видимости линии пересечения поверхностей на горизонтальной проекции. Для этой цели использовалась вспомогательная секущая плоскость b, которая пересекает поверхность Q по линии m, а поверхность G по образующим, горизонтальные проекции которых пересекаясь определяют положение искомых точек.

Соединив найденные точки 1...10 с учетом видимости получим линию пересечения поверхностей.

Вторым примером использования в качестве вспомогательных поверхностей посредников концентрических сфер рассмотрим при определении линии пересечения поверхностей предложенных на рисунке 8.34. Оси поверхностей вращения G и Q пересекаются в точки А , при этом ось поверхности Q - фронтально проецирующая прямая, а ось поверхности G - горизонталь. Точка А принимается за центр всех вспомогательных концентрических сфер.

Точки 1 и 2 линии пересечения построены с помощью сферы радиуса R. Эта сфера пересекает поверхность Q по окружности а, а поверхность G по окружности в, которая показана только на горизонтальной проекции. Пересечение горизонтальных проекций окружностей а₁ и в₁ определяют проекции 1₁ и 2₁ точек линии пересечения. Их фронтальные проекции 1₂ и 2₂построены на а₂ пересечении с линиями связи.

Аналогично найдены точки 3 и 4.

Для нахождения точек 5 и 6 определяющих границу зоны видимости на горизонтальной проекции использовалась вспомогательная секущая плоскость b, которая пересекает поверхность Q по окружность n, а коническую поверхность G по треугольнику определяющему ее очерк на горизонтальной проекции.

Точки 7 и 8 находятся на границе зоны видимости фронтальной проекции, для их нахождения используется вспомогательная секущая плоскость g.

Соединив найденные точки 1...8 с учетом видимости получим линию пересечения поверхностей G и Q.

Рисунок 8.34. Пересечение
поверхностей вращения, ось одной - горизонтально проецирующая прямая, а второй - горизонталь

*Эксцентрические сферические посредники* применяются при определении точек линии пересечения поверхностей вращения с поверхностью несущей на себе непрерывное множество окружностей. Обе поверхности должны иметь общую плоскость симметрии. Вспомогательные эксцентрические сферы пересекаются с данными поверхностями по окружностям.

	а) модель	б) эпюр
Рисунок 8.35. Пересечение конуса и сферы

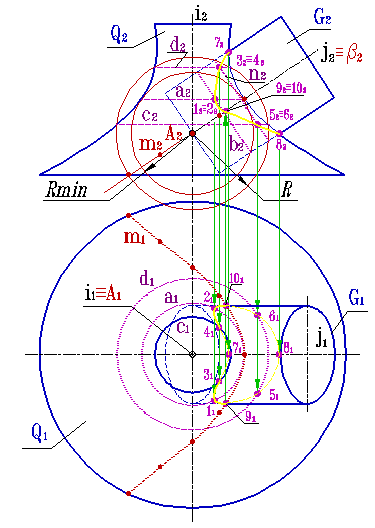
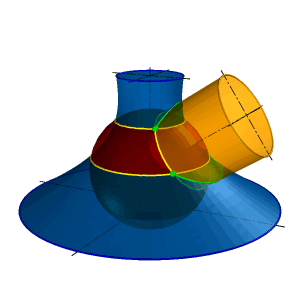
Определения линии пересечения конуса и сферы применение эксцентричных сфер, как поверхностей - посредников. Центры сфер - точки расположены на оси конуса. Сфера пересекает конус и сферу по окружностям , которые пересекаются в двух точках, принадлежащих искомой линии пересечения (рис.8.35а).

Верхняя и нижняя точки линии пересечения найдены с помощью вспомогательной секущей плоскости - плоскости главного фронтального меридиана, пересекающая конус и сферу по треугольнику и окружности, являющимися очерками поверхностей на фронтальной плоскости проекций.

Точки определяющие границу зоны видимости линии пересечения на горизонтальной плоскости проекций, найдены с помощью вспомогательной секущей плоскости - горизонтальной плоскости уровня, пересекающей сферу по экватору - окружности являющейся очерком шара на горизонтальной проекции, а конус по окружности - параллели.

Найденные с помощью вспомогательных поверхностей посредников точки определяют линию пересечения конуса и шара.

Рассмотрим на примере определения линии пересечения конуса Q и сферы G (рис.8.35б) применение эксцентричных сфер, как поверхностей - посредников. Центры сфер - точки А¹, А² и А³ расположены на оси конуса. Сфера радиуса R¹ с центром в точке А¹ пересекает конус и сферу по окружностям аи в, которые пересекаются в точках 1 и 2, принадлежащих искомой линии пересечения. С помощью сферы R² с центром А²и сферы R³ с центром А³ определено положение точек 3, 4 и 5,6 соответственно. Точки 7 и 8 найдены с помощью вспомогательной секущей плоскости a (плоскости фронтального меридиана), пересекающая конус и сферу по главном фронтальном меридианам k и l. Точки 9 и 10, определяющие границу зоны видимости линии пересечения на горизонтальной плоскости проекций, найдены с помощью вспомогательной секущей плоскости b (горизонтальной плоскости уровня), пересекающей сферу G по экватору s, а конус Q по окружности p. Найденные с помощью вспомогательных поверхностей посредников точки 1...10 определяют линию пересечения конуса и шара.

Частные случаи пересечения поверхностей второго порядка

Поверхностью второго порядка называется множество точек пространства, декартовы координаты, которых удовлетворяют алгебраическому уравнению второй степени.

Две поверхности второго порядка в общем случае пересекаются по пространственной линии четвертого порядка, которую называют биквадратной кривой.

В некоторых случаях биквадратная кривая распадается на две плоские кривые второго порядка, причем одна из них может быть мнимой.

Опуская доказательства, приведем некоторые теоремы и примеры, иллюстрирующие их применение.

Теорема 1. Если две поверхности второго порядка пересекаются по одной плоской кривой, то существует и другая плоская кривая, по которой они пересекаются.

Рассмотрим пример, к которому приложима теорема.

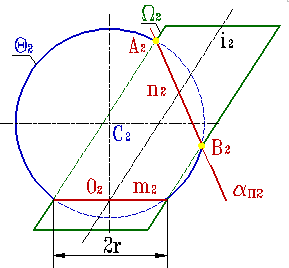
Фронтальные проекции q₂ сферы Q и W₂ эллиптического цилиндра W, имеющих общую окружность m(m₂) с центром О(О₂) (рис.8.36).


	а) модель	б) эпюр
Рисунок 8.36. Пересечение сферы и эллиптического цилиндра

Плоскость σ, определяемая центром сферы С и осью i цилиндра, является плоскостью симметрии заданных поверхностей, и параллельна фронтальной плоскости проекций.

Общая окружность радиуса r – это одна из плоских кривых второго порядка распавшейся линии пересечения. Остается построить вторую кривую, плоскость α которой должна быть в условиях данного примера перпендикулярна плоскости симметрии σ, а следовательно и П₂. Вторая линия пересечения (окружность) проецируется на П₂ в виде отрезка прямой n₂. Для ее построения следует воспользоваться точками А₂ и В₂, принадлежащими очеркам заданных поверхностей.

Теорема 2.(о двойном касании). Если две поверхности второго порядка имеют касание в двух точках А и В, то линия их пересечения распадается на две плоские кривые второго порядка, плоскость которых проходит через отрезок АВ, соединяющий точки касания.


	а) модель	б) эпюр
Рисунок 8.37 Пересечение сферы и эллиптического цилиндра имеющих две точки касания

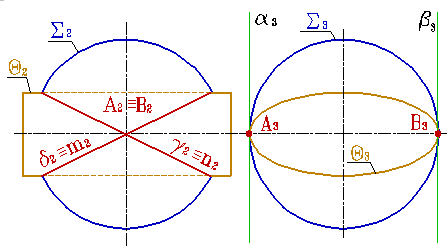
Например, по двум окружностям m и n пересекается сфера S и эллиптический цилиндр Q (рис.8.37). Точки касания и касательные плоскости обозначены соответственно через А, В, α, β. Окружности, на которые распалась линия пересечения поверхностей, расположены во фронтально- проецирующих плоскостях γ и δ.

Теорема 3. (теорема Г. Монжа). Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки линий касания.


	а) модель	б) эпюр
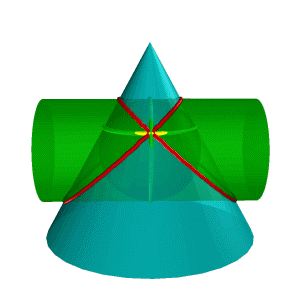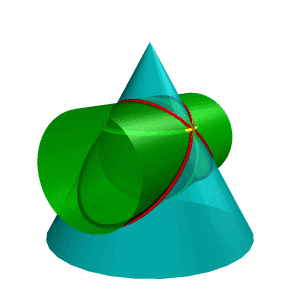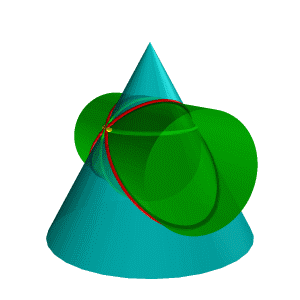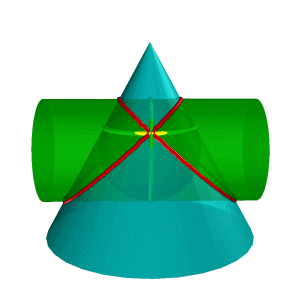
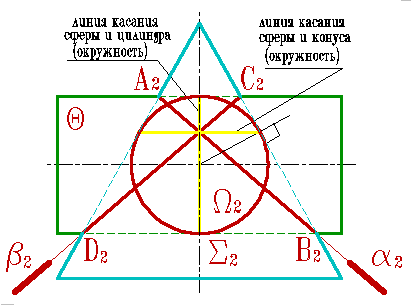
Рисунок 8.38. Пересечение конуса и цилиндра имеющих общую вписанную сферу

В соответствии с этой теоремой линия пересечения конуса Σ и цилиндра Q (рис.8.38), описанных около сферы W, будут плоскими кривыми – эллипсами (расположенными в плоскостях a и b), фронтальные проекции которых изображаются прямыми А₂В₂ и С₂Д₂,

Теорема Монжа находит эффективное применение при конструировании трубопроводов.

Теорема 4. Если две поверхности второго порядка имеют общую плоскость симметрии, то линия их пересечения проецируется на эту плоскость в виде кривой второго порядка.


	а) модель	б) эпюр
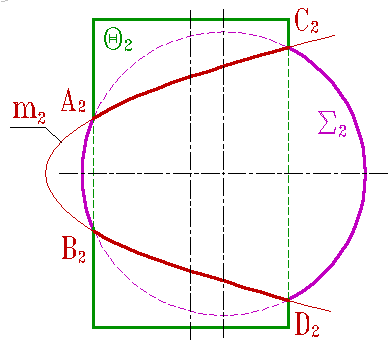
Рисунок 8.39. Пересечение сферы и цилиндра

Плоскость симметрии определена осью симметрии цилиндра Q и центром сферы S (рис.8.39). Плоскости принадлежат и симметричные сами себе точки A, B, C и D линий пересечения. Проекция же линий на фронтальную плоскость имеет форму параболы m₂ и аналитически описывается формулой параболы.

Задачи на тему "Поверхность"